Fibonacci数列为什么经常出现在植物中
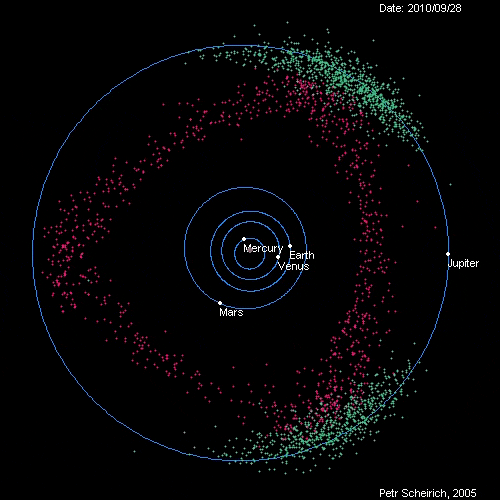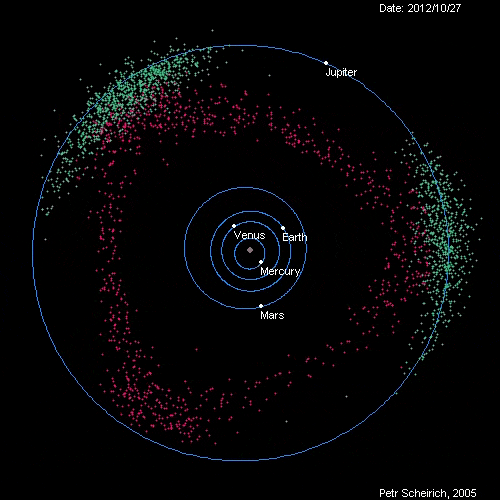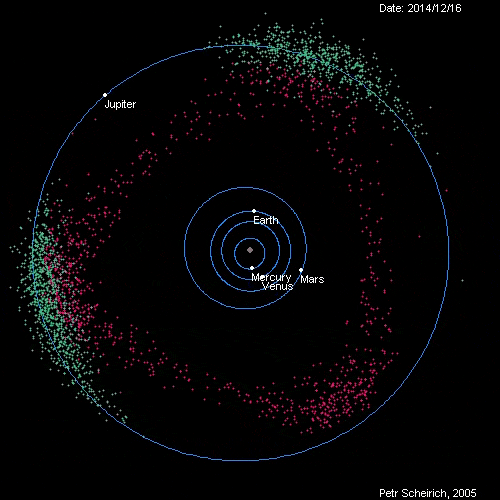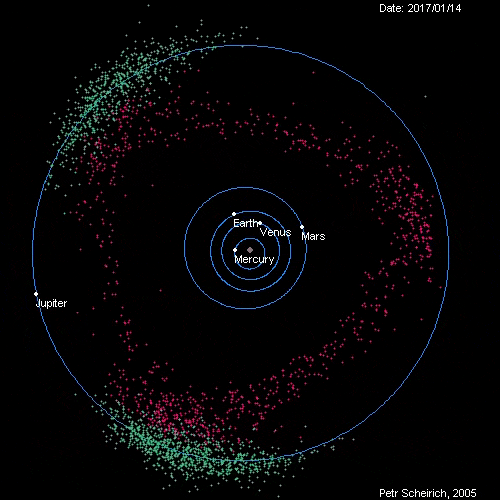
拾起一个松果仔细观察(你问为什么要这么做?如果你不问这个问题而是把这个动作重复上40次,说不定已经发nature了= =注:传说有人去山上捡了40个松果,统计出左旋和右旋型的松果数量是基本相同的,于是发了篇nature[1]),我们至少能在其上找到两种旋转方向相反的螺线。若有人闲得蛋疼,非要数一数这样的螺线有多少条,就图一中的例子来说,是8和13。我们在向日葵的头状花序上也能见到这样的螺线,并且同样可以找出旋转方向相反的两种(通过改变线的连接方式,你也可以找出更多这样的螺线)。数一下条数,小的是13和21,大的是21和34。这些数字看起来似乎不是任意的,彼此之间还有些关联。比如8+13=21,,13+21=34。正如标题所说,这些数字都是Fibonacci数列{1,1,2,3,5,8,13,21,34……}的一部分,并且两种方向相反的螺线数还是Fibonacci数列种相邻的两个数字。把视线稍微放宽一点,植物叶子的排列方式,叫做叶序。最常见的有互生,对生和轮生。如果我们只观察互生(互生的特点是每个节上只有一片叶子),从茎生长的方向垂直看下来,相邻叶片之间往往相差(旋转了)一个角度,从下往上数叶片的数量,直至新数到的叶片角度与初始叶片完全重合。例如在数的过程中叶片转过3圈,共有8片叶子,称为3/8叶序(螺旋叶序)。橡树和梨树的叶序就为3/8,椴树的叶序为1/2,柳树为5/13[4]。从中我们依旧看到Fibonacci数的身影。那为什么植物中存在着这么多的Fibonacci数呢?… 阅读全文